
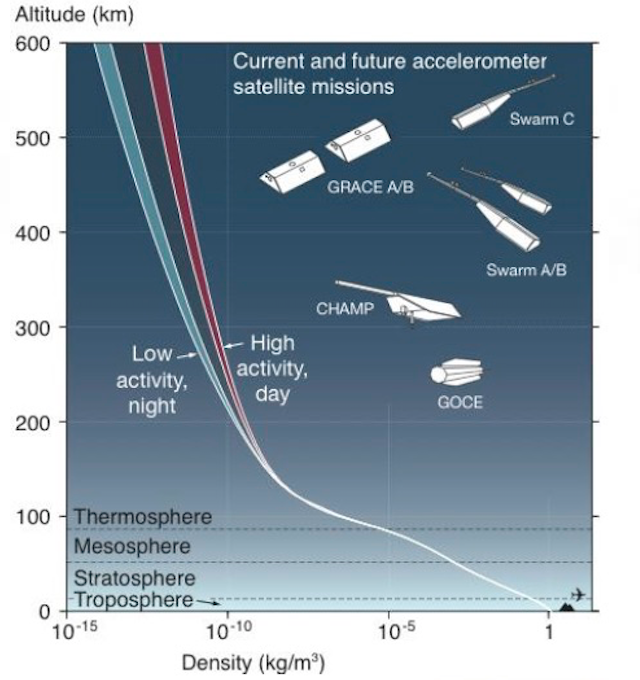
Generally, aircraft performance-in terms of lift generated by the wing, and thrust generated by the engine-decreases with an increase in ambient temperature and a decrease in ambient air pressure. There are many occasions in which a pilot has to predict the performance of an aircraft-e.g., in planning a takeoff, in planning a climb over mountainous terrain, in predicting rates of fuel consumption, and aircraft performance with respect to speed. Students / Resources / Classroom / Private Pilot Groundschool /.Look at table 1-6 and find the standard temperature corresponding to 2,000 feet. For example, let's say the surface temperature is 30☌ and your pressure altitude is 2,010 feet. If you are in a situation where you do not have a density altitude computer or the Smithsonian Meteorological Tables available, you may ignore the humidity value and calculate density altitude by the formula DA = PA + (120 V t ), where DA = density altitude, PA = pressure altitude at the level you desire density altitude, 120 = a temperature constant (120 feet per 1☌), and V t = actual temperature minus standard temperature at the level of the pressure altitude. Density altitude results from the computer may be estimated to the nearest 10 feet between the marked increments of 100 feet. Specific instructions are printed on the device. Density altitude must be computed from the pressure (for takeoff, station pressure) and the virtual temperature at the particular altitude under consideration. The quickest method of calculating density altitude is to use the Density Altitude Computer (CP-718/UM), discussed in chapter 2. Remember, virtual temperature is used in the computation of density altitude.

This may be accomplished by using the Density Altitude Computer (CP-718/UM) or from Table 69, Density Altitude Diagram, of Smithsonian Meteorological Tables, NA-50-lB-521. It must be computed from the pressure (for takeoff, station pressure) and the virtual temperature at the particular altitude under consideration. No instrument is available to measure density altitude directly. True airspeed exceeds indicated airspeed when density altitude increases. True airspeed and indicated airspeed are equal only when density altitude is zero. Therefore, the air is less dense than normal, and an aircraft on takeoff (at approximately constant weight and power setting) will take longer to get airborne. If, for example, the pressure at Cheyenne, Wyoming, (elevation 6,140 feet) is equal to the pressure of the standard atmosphere at that elevation, and the temperature is 101☏, the density would be the same as that found at 10,000 feet. Changes in pressure and temperature have the greatest effect on density altitude, and changes in humidity have the least effect. An increase in humidity decreases air density, so itincreases density altitude. An increase in temperature decreases air density, so it increases density altitude. An increase in pressure increases air density, so it decreases density altitude. For a given altitude, density altitude changes with changes in pressure, air temperature, and humidity. DENSITY ALTITUDE Density altitude is defined as the altitude at which a given air density is found in the standard atmosphere. Maximum pressure altitude may be used by the pilot in lieu of density altitude. Many rotary wing aircraft have a table in their aircraft technical data that is entered using maximum pressure altitude and maximum temperature to find the maximum permissible load that can be carried. The forecaster may have to interpret the other stations forecast to determine if the forecast QNH will be valid during the time the aircraft will be in the vicinity. This is calculated using the lowest expected altimeter setting (QNH) for the destination.
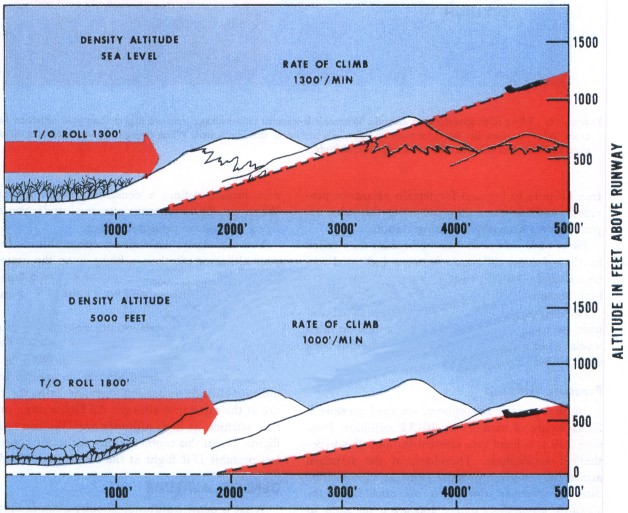
Pilots of aircraft, especially rotary wing aircraft, frequently ask for maximum pressure altitude for takeoff and for all destinations. With the pressure reduction computer, the same case yields a pressure altitude of 1,979 feet. And, it may be done quickly in your head. For example, using the formula for the same case we just calculated with the table, we find the following: PA= H A + PAV PA = 1,500 + 1,000(29.92 - 29.41) PA = 1,500 + 510 PA = 2,010 feet By comparison, you can see that this value is 34 feet higher than we found by using the table, but it is a close enough approximation when nothing else is available.


 0 kommentar(er)
0 kommentar(er)
